Will A Piece Of Paper, Folded 42 Times, Reach The Moon?
So I was at a friend's house Sunday night playing a game when this odd fact came up in conversation:
If you were to fold a piece of paper in half 42 times, it would reach the moon.
Several of those around the table scoffed at this, exclaiming that a single sheet of paper was simply too thin to have its thickness reach any substantial amount after only a few dozen folds. I pointed out it was entirely possible seeing as how doubling the thickness with each fold would lead to an exponential increase in thickness that would increase slowly at first before quickly getting larger. My friends were clearly imagining a linear increase in thickness.
I also knew that it is pretty much impossible to fold a single sheet of paper more than about 8 times -- though Myth Busters once folded a giant sheet the size of a football field 10 times. The resulting thickness (after hitting it with a bulldozer) was almost a foot tall, though there was quite a bit of air mixed in with the 1,024 sheets. The formula for finding out how many of something you'll have after doubling it N number of times is as follows where O is the original number (or size in our case).
o * 2^(n)
A standard sheet of paper is about 0.1 mm so 42 folds would give us this:
0.1 * 2^(42) = 439,804,651,110 mm
That's 440 billion millimeters, or 439,804 kilometers. The moon on average is 384,400 kilometers from Earth according to Google. I'd say this checks out.
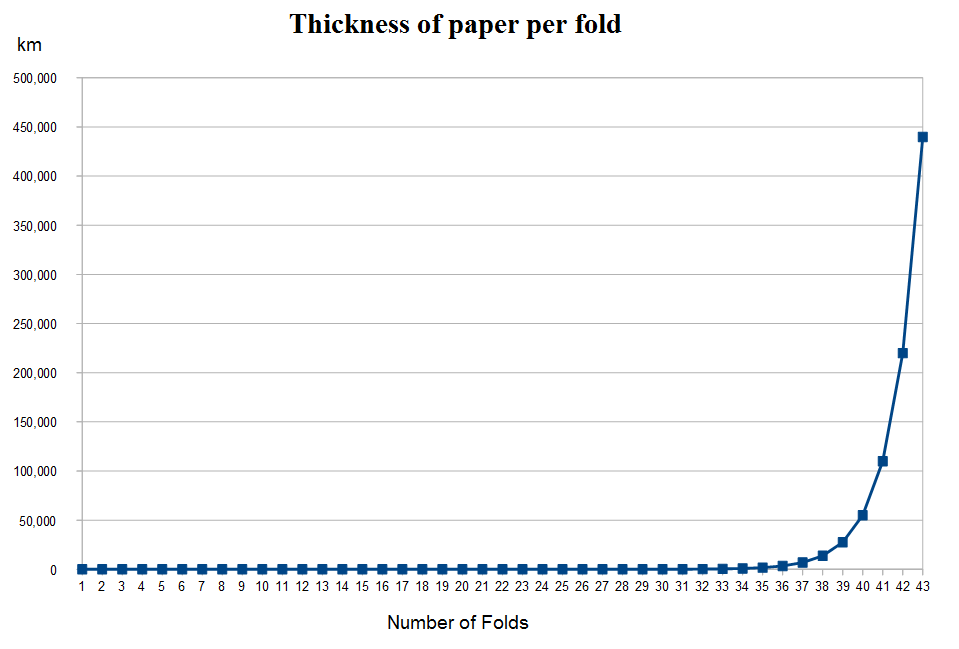
To help visualize the data, I created a quick spreadsheet and graph that tracks the thickness of the paper for each fold.
| # Folds | Thickness (mm) |
| 0 | 0.10 |
| 1 | 0.20 |
| 2 | 0.40 |
| 3 | 0.80 |
| 4 | 1.60 |
| 5 | 3.20 |
| 6 | 6.40 |
| 7 | 12.80 |
| 8 | 25.60 |
| 9 | 51.20 |
| 10 | 102.40 |
| 11 | 204.80 |
| 12 | 409.60 |
| 13 | 819.20 |
| 14 | 1,638.40 |
| 15 | 3,276.80 |
| 16 | 6,553.60 |
| 17 | 13,107.20 |
| 18 | 26,214.40 |
| 19 | 52,428.80 |
| 20 | 104,857.60 |
| 21 | 209,715.20 |
| 22 | 419,430.40 |
| 23 | 838,860.80 |
| 24 | 1,677,721.6 |
| 25 | 3,355,443.2 |
| 26 | 6,710,886.4 |
| 27 | 13,421,773 |
| 28 | 26,843,546 |
| 29 | 53,687,091 |
| 30 | 107,374,182 |
| 31 | 214,748,365 |
| 32 | 429,496,730 |
| 33 | 858,993,459 |
| 34 | 1,717,986,918 |
| 35 | 3,435,973,837 |
| 36 | 6,871,947,674 |
| 37 | 13,743,895,347 |
| 38 | 27,487,790,694 |
| 39 | 54,975,581,389 |
| 40 | 109,951,162,778 |
| 41 | 219,902,325,555 |
| 42 | 439,804,651,110 |
And to graph that out in kilometers looks like this:
rodger d'odger
Brad - interesting bit of stuff. I read within the last 5-8 years that some young lady won quite a bit of fame by folding a speciallly constructed piece of paper around 15 times. Most of us have been fed a bit of "trust me" when told it couldn't be done more than 8.
However, I'd like to find out how big this piece of paper needs to be And how much it would weigh. Would the weight compress the paper so it might not reach the moon?
And why is this tiny "Comment:" text box so small?
Brad Wood
@Roger - I suppose if you started with a very large and VERY thin sheet of paper you might get close to 15 folds, but one of the issues is that the size of the paper also shrinks by 50% with each fold. That Myth Busters episode I mentioned started with a sheet the size of a football field and after 10 folds, it was only about 4 or 5 feet wide.
> Would the weight compress the paper so it might not reach the moon?
I'm afraid that despite the theoretical concept of paper touching the moon, there would be more than a few physics and logistics issues. You'd probably need to start with a sheet roughly the size of the milky way. And at that point, the paper would most likely have more mass than the Earth, which means it would be compressing the Earth, not the other way around :)
Tom
This is one of those "if" "then" subjects. Yeah if you had a piece of paper that large then if you were to fold it that many times? That's rediculous! Because I could run around the earth in 20 minutes if I had legs that were 30,000 feet long. The truth is, standard paper is 8.5 x 11" so there goes you theory because you could never fold it enough to prove this! If only then maybe??
Vishal Achari
This is really amazing thinking. Hats off man!
roger tubby
Of course. That's the answer (42). Just think, humanity - at least in Douglas Adams' world would have saved several 10's of thousands of years if we had your calculation, Brad.
Sahil Kumar
With a slight variation, this could be tested practically. Instead of folding the paper, cut the paper and stack the cut pieces in layers. You probably want to do that inside of a very narrow tube. My feeling is that you would be dividing molecules long before you reached the Moon, likely before you reached 50 meters. I don’t have a good idea how high the stack would be before you were dividing atoms, but probably short of the Moon and the thickness of the paper would have stopped mattering long before then. This is an exercise that only makes sense in a situation where the paper remains paper no matter how many times it is cut or folded. In other words, fantasy land.
jessica
this is mind blowing!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!